Reflexive Property Of Congruence Example

Proving Triangles Congruent Using Definition of Congruent Triangles – Part 2

Posted on Nov one, 2009 by Mr. Pi

Office one of Congruent Figures four.1

Role 2 of Congruent Figures Proving Triangles Congruent

The 3rd part of this series virtually congruent figures is proving triangles coinciding. At this signal, there is only one style to evidence triangles congruent, with the definition of congruent triangles. Coinciding triangles take 3 pairs of respective angles and iii pairs of congruent angles. So, to prove 2 triangles congruent, we must establish that all 3 pairs of respective sides and angles are congruent.

Given: segment WX is coinciding to YX, segment WZ is coinciding to segment YZ, angle W is congruent to angle Y and segment XZ is perpendicular to segment WY

Prove: triangle WXZ is congruent to triangle YXZ

Proving Triangles Congruent Diagram 4.1

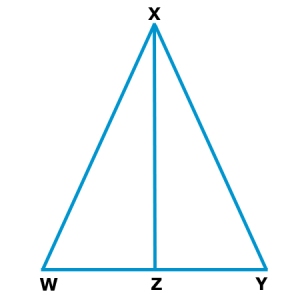
With the given information: segment WX is congruent to YX, segment WZ is congruent to segment YZ, bending W is coinciding to angle Y and segment XZ is perpendicular to segment WY, prove triangle WXZ is congruent to triangle YXZ. First, segment XZ is congruent to segment XZ by the reflexive holding of congruence. Angles XZW and XZY are right angles past the definition of right angles. Bending XZW and angle XZY are congruent considering all correct angles are congruent. Bending WXZ is congruent to angle YXZ by the 3rd angle theorem. It can exist established that triangle WXZ is congruent to triangle YXZ past the definition of coinciding triangles.

Filed under: Geometry, Proving Triangles Congruent | Tagged: Geometry, Proving Triangles Congruent, reflexive property of congruence, third bending theorem | Leave a comment »

Proving Triangles Congruent Using Definition of Coinciding Triangles

Posted on November 1, 2009 by Mr. Pi

The second role of this serial about congruent figures is proving triangles congruent. If you are interested in the reading the first mail on Coinciding Figures. At this point, there is only ane style to prove triangles congruent, with the definition of congruent triangles. Congruent triangles have 3 pairs of respective angles and 3 pairs of coinciding angles. So, to evidence two triangles congruent, we must establish that all three pairs of corresponding sides and angles are congruent. The third angle theorem states, if ii angles of one triangle are congruent to ii angles of another triangle, the third angles are congruent to each other.

Given: segment AB is congruent to segment AD, segment BC is coinciding to segment DC, angle B is congruent to angle D, and bending BAC is congruent angle DAC

Prove: triangle ABC is congruent to triangle ADC

Proving Triangles Congruent Section 4.1

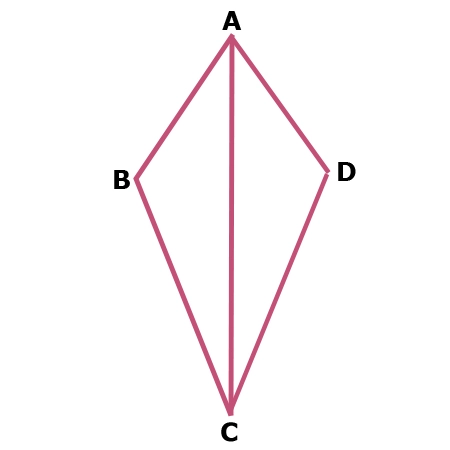
Prove Triangle ABC congruent to Triangle ADC

With the given data: segment AB is congruent to segment Advertising, segment BC is congruent to segment DC, angle B is congruent to bending D, and angle BAC is congruent angle DAC, prove triangle ABC is congruent to triangle ADC. Segment Ac is coinciding to segment AC past the reflexive property of congruence. Side by side, it must be established that angle ACB is congruent to bending ACD, past the third angle theorem. Since, all three pairs of corresponding sides and angles are congruent, triangle ABC is congruent to triangle ADC.

Filed nether: Geometry, Proving Triangles Congruent | Tagged: Definition of coinciding triangles, Geometry, Proving Triangles Congruent, reflexive belongings of congruence, third angle theorem | four Comments »